设椭圆 :
:  的离心率为
的离心率为 ,点
,点 (
( ,0),
,0), (0,
(0, )原点
)原点 到直线
到直线 的距离为
的距离为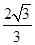 。
。
(1) 求椭圆 的方程;
的方程;
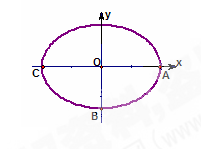
(2) 设点 为(
为( ,0),点
,0),点 在椭圆
在椭圆 上(与
上(与 、
、 均不重合),点
均不重合),点 在直线
在直线 上,若直线
上,若直线 的方程为
的方程为 ,且
,且 ,试求直线
,试求直线 的方程.
的方程.
推荐套卷
设椭圆 :
:  的离心率为
的离心率为 ,点
,点 (
( ,0),
,0), (0,
(0, )原点
)原点 到直线
到直线 的距离为
的距离为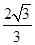 。
。
(1) 求椭圆 的方程;
的方程;
(2) 设点 为(
为( ,0),点
,0),点 在椭圆
在椭圆 上(与
上(与 、
、 均不重合),点
均不重合),点 在直线
在直线 上,若直线
上,若直线 的方程为
的方程为 ,且
,且 ,试求直线
,试求直线 的方程.
的方程.