2013年我国汽车拥有量已超过2亿(目前只有中国和美国超过2亿),为了控制汽车尾气对环境的污染,国家鼓励和补贴购买小排量汽车的消费者,同时在部分地区采取对新车限量上号.某市采取对新车限量上号政策,已知2013年年初汽车拥有量为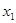 (
(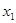 =100万辆),第
=100万辆),第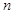 年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为
年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为 ,该年的增长量
,该年的增长量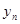 和
和 与
与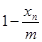 的乘积成正比,比例系数为
的乘积成正比,比例系数为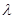
 其中
其中 =200万.
=200万.
(1)证明: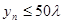 ;
;
(2)用 表示
表示 ;并说明该市汽车总拥有量是否能控制在200万辆内.
;并说明该市汽车总拥有量是否能控制在200万辆内.
相关知识点
推荐套卷
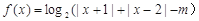 .
.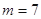 时,求函数
时,求函数 的定义域;
的定义域;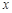 的不等式
的不等式 的解集是
的解集是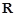 ,求
,求 的取值范围.
的取值范围.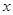 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线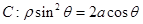
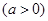 ,过点
,过点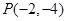 的直线
的直线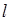 的参数方程为
的参数方程为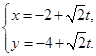 (t为参数)。直线
(t为参数)。直线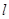 与曲线
与曲线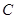 分别交于
分别交于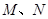 .若
.若 成等比数列,求实数
成等比数列,求实数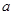 的值。
的值。 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的平分线
的平分线 交⊙
交⊙ ,过点
,过点 交
交 ,
, 交
交 .若
.若 ,求
,求 的值。
的值。
 的椭圆记作C2
的椭圆记作C2
 ,是否存在定圆
,是否存在定圆 ,使得
,使得 (a是实数),
(a是实数), +1。
+1。 时,求函数
时,求函数 在定义遇上的最值.
在定义遇上的最值. )上是单调函数,求a的取值范围;
)上是单调函数,求a的取值范围; ,总存在
,总存在 ,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。 粤公网安备 44130202000953号
粤公网安备 44130202000953号