如图，三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形，且侧面AA1C1C是边长为2的正方形,E是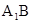
的中点,F在棱CC1上。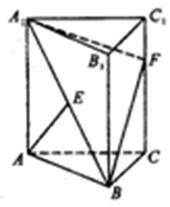
（1）当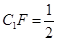
CF时，求多面体ABCFA1的体积；
（2）当点F使得A1F+BF最小时，判断直线AE与A1F是否垂直，并证明的结论。
相关试题
在
上是减函数；
的最小正周期和值域；
，且
，求
的值.
的单调性；
和
，记过点
的直线的斜率为
，问：是否存在
，使得
？若存在，求出
，
，求
在
处的切线方程；（II）求
上的最小值.
为选出的4名选手中女选手的人数，求相关知识点
推荐套卷
如图，三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形，且侧面AA1C1C是边长为2的正方形,E是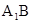的中点,F在棱CC1上。
（1）当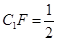CF时，求多面体ABCFA1的体积；
（2）当点F使得A1F+BF最小时，判断直线AE与A1F是否垂直，并证明的结论。
粤公网安备 44130202000953号