如图，抛物线y=ax2+bx+c经过点A（﹣3，0），B（0，3），C（1，0）．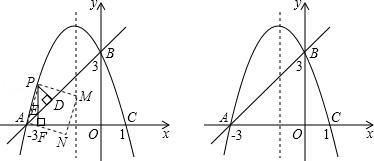
（1）求此抛物线的解析式．
（2）点P是直线AB上方的抛物线上一动点，（不与点A、B重合），过点P作x轴的垂线，垂足为F，交直线AB于点E，作PD⊥AB于点D．
①动点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；
②连接PA，以AP为边作图示一侧的正方形APMN，随着点P的运动，正方形的大小、位置也随之改变．
当顶点M或N恰好落在抛物线对称轴上时，求出对应的P点的坐标．（结果保留根号）
相关试题
为实施“农村留守儿童关爱计划”，某校结全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：
（1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；
（2）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．
，BD∥CE，连接AE并延长交BD于D．求证：
相关知识点
推荐套卷
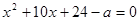粤公网安备 44130202000953号