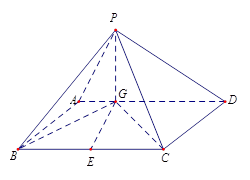
如图四棱锥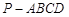 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,垂足为
,垂足为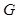 ,
,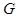 在
在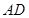 上且
上且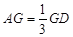 ,
, ,
,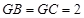 ,
,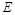 是
是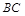 的中点,四面体
的中点,四面体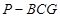 的体积为
的体积为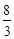 .
.
(1)求二面角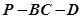 的正切值;
的正切值;
(2)求直线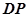 到平面
到平面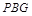 所成角的正弦值;
所成角的正弦值;
(3)在棱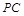 上是否存在一点
上是否存在一点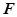 ,使异面直线
,使异面直线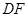 与
与 所成的角为
所成的角为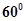 ,若存在,确定点
,若存在,确定点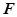 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
推荐套卷
如图四棱锥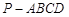 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,垂足为
,垂足为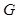 ,
,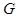 在
在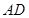 上且
上且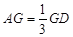 ,
, ,
,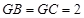 ,
,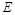 是
是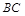 的中点,四面体
的中点,四面体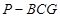 的体积为
的体积为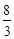 .
.
(1)求二面角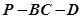 的正切值;
的正切值;
(2)求直线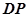 到平面
到平面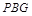 所成角的正弦值;
所成角的正弦值;
(3)在棱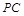 上是否存在一点
上是否存在一点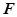 ,使异面直线
,使异面直线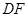 与
与 所成的角为
所成的角为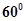 ,若存在,确定点
,若存在,确定点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.