如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.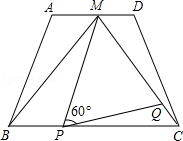
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;
(3)在(2)中:
①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当y取最小值时,判断△PQC的形状,并说明理由.
相关知识点
推荐套卷

 上;
上;  时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;
时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;
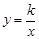 的图象经过(1,-2).
的图象经过(1,-2).
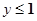 时,
时,
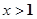 时,y的取值范围.
时,y的取值范围.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号