湖南省在学业水平考查中设计了物理学科的实验考查方案:考生从 道备选试验考查题中一次随机抽取
道备选试验考查题中一次随机抽取 题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中
题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中 题便通过考查.已知
题便通过考查.已知 道备选题中文科考生甲有
道备选题中文科考生甲有 题能正确完成,
题能正确完成, 题不能完成;文科考生乙每题正确完成的概率都是
题不能完成;文科考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(Ⅰ)分别写出文科考生甲正确完成题数 和文科考生乙正确完成题数
和文科考生乙正确完成题数 的概率分布列,并计算各自的数学期望;
的概率分布列,并计算各自的数学期望;
(Ⅱ)试从两位文科考生正确完成题数的数学期望及通过考查的概率分析比较这两位考生的实验操作能力.
相关知识点
推荐套卷
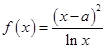 (其中a为常数).
(其中a为常数).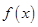 的3个极值点为
的3个极值点为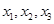 ,且
,且 .证明:
.证明: .
. ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为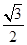 的椭圆过点
的椭圆过点

 与该椭圆交于
与该椭圆交于 两点,满足直线
两点,满足直线 的斜率依次成等比数列,求
的斜率依次成等比数列,求 面积的取值范围.
面积的取值范围. .
.
 ,在直线AC上是否存在一点D,使得直线BD与平面PBC所成角为30°?若存在,求出CD的长;若不存在,说明理由.
,在直线AC上是否存在一点D,使得直线BD与平面PBC所成角为30°?若存在,求出CD的长;若不存在,说明理由.
 的对边分别为
的对边分别为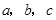 .已知
.已知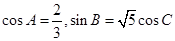 .
. 的值;
的值;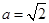 ,求边
,求边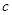 的长及
的长及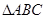 的面积.
的面积. 粤公网安备 44130202000953号
粤公网安备 44130202000953号