设集合W是满足下列两个条件的无穷数列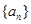 的集合:①对任意
的集合:①对任意 ,
, 恒成立;②对任意
恒成立;②对任意 ,存在与n无关的常数M,使
,存在与n无关的常数M,使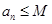 恒成立.
恒成立.
(1)若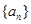 是等差数列,
是等差数列,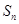 是其前n项和,且
是其前n项和,且 试探究数列
试探究数列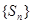 与集合W之间的关系;
与集合W之间的关系;
(2)设数列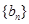 的通项公式为
的通项公式为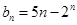 ,且
,且 ,求M的取值范围.
,求M的取值范围.
相关知识点
推荐套卷
设集合W是满足下列两个条件的无穷数列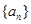 的集合:①对任意
的集合:①对任意 ,
, 恒成立;②对任意
恒成立;②对任意 ,存在与n无关的常数M,使
,存在与n无关的常数M,使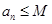 恒成立.
恒成立.
(1)若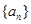 是等差数列,
是等差数列,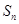 是其前n项和,且
是其前n项和,且 试探究数列
试探究数列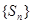 与集合W之间的关系;
与集合W之间的关系;
(2)设数列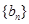 的通项公式为
的通项公式为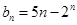 ,且
,且 ,求M的取值范围.
,求M的取值范围.