如图，在平面直角坐标系的第一象限中，有一各边所在直线均平行于坐标轴的矩形ABCD，且点A在反比例函数L1：y＝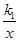
(x＞0) 的图象上，点C在反比例函数L2：y＝
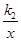(x＞0) 的图象上（矩形ABCD夹在L1与L2之间）．（1）若点A坐标为（1,1）时，则L1的解析式为 ．（2）在（1）的条件下，若矩形ABCD是边长为1的正方形，求L2的解析式．（3）若k1＝1，k2＝6，且矩形ABCD的相邻两边分别为1和2，求符合条件的顶点C的坐标．
相关试题
－1=
，去分母时方程左边的1没有乘以10,由此求得方程的解为x=4，试求a的值，并正确求出方程的解。
)
+
=0，求2x－
的值。
]，[
]，[
]，…，[
]。相关知识点
推荐套卷
粤公网安备 44130202000953号