已知椭圆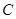 的中心为直角坐标系
的中心为直角坐标系 的原点,焦点在
的原点,焦点在 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆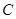 的方程;
的方程;
(2)若 为椭圆
为椭圆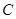 的动点,
的动点, 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点,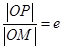 (
(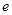 为椭圆的离心率),求点
为椭圆的离心率),求点 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
推荐套卷
已知椭圆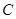 的中心为直角坐标系
的中心为直角坐标系 的原点,焦点在
的原点,焦点在 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆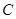 的方程;
的方程;
(2)若 为椭圆
为椭圆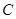 的动点,
的动点, 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点,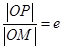 (
(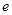 为椭圆的离心率),求点
为椭圆的离心率),求点 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.