某营养师要为某个儿童预订午餐和晚餐，已知一个单位的午餐含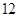
个单位的碳水化合物，
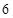个单位的蛋白质和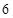个单位的维生素
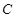；一个单位的晚餐含
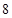个单位的碳水化合物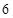，个单位的蛋白质和
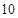个单位的维生素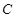.另外，该儿童这两餐需要的营养中至少含
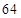个单位的碳水化合物，
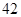个单位的蛋白质和
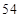个单位的维生素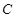.如果一个单位的午餐、晚餐的费用分别是
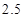元和
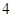元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？
相关试题
是双曲线
的左，右焦点,点
是双曲线右支上的一个动点,且
的最小值为
,双曲线的一条渐近线方程为
. 求双曲线的方程;
和双曲线
有公共的焦点，（1）求双曲线的渐近线方程（2）直线
过焦点且垂直于x轴，若直线
，求双曲线的方程
的左，右焦点分别为
，点P在双曲线的右支上，且
，求此双曲线的离心率e的最大值．
－
=1有公共焦点，且过点（3
，2）.求双曲线C的方程．推荐套卷
某营养师要为某个儿童预订午餐和晚餐，已知一个单位的午餐含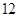个单位的碳水化合物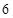，个单位的蛋白质和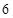个单位的维生素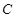；一个单位的晚餐含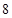个单位的碳水化合物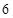，个单位的蛋白质和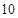个单位的维生素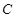.另外，该儿童这两餐需要的营养中至少含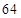个单位的碳水化合物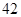，个单位的蛋白质和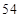个单位的维生素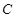.如果一个单位的午餐、晚餐的费用分别是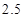元和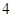元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？
粤公网安备 44130202000953号