已知偶函数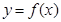 满足:当
满足:当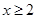 时,
时,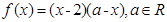 ,当
,当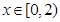 时,
时,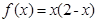 .
.
(Ⅰ)求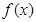 表达式;
表达式;
(Ⅱ)若直线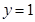 与函数
与函数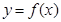 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数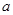 的取值范围;
的取值范围;
(Ⅲ)试讨论当实数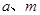 满足什么条件时,直线
满足什么条件时,直线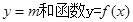 的图像恰有
的图像恰有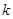 个公共点
个公共点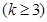 ,且这
,且这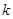 个公共点均匀分布在直线
个公共点均匀分布在直线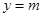 上.(不要求过程)
上.(不要求过程)
相关知识点
推荐套卷
已知偶函数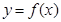 满足:当
满足:当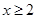 时,
时,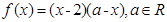 ,当
,当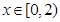 时,
时,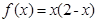 .
.
(Ⅰ)求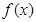 表达式;
表达式;
(Ⅱ)若直线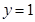 与函数
与函数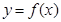 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数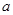 的取值范围;
的取值范围;
(Ⅲ)试讨论当实数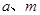 满足什么条件时,直线
满足什么条件时,直线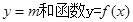 的图像恰有
的图像恰有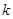 个公共点
个公共点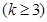 ,且这
,且这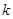 个公共点均匀分布在直线
个公共点均匀分布在直线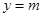 上.(不要求过程)
上.(不要求过程)