已知二次函数f(x)=x2+ax（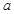
）．
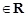（1）若函数y=f(sinx+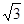
cosx)(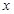
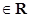)的最大值为
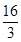，求f(x)的最小值；
（2）当a>2时,求证：f(sin2xlog2sin2x+cos2xlog2cos2x)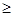
1–a.其中x∈R,x¹kp且x¹kp
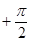(k∈Z).
相关试题
是
的极值点，求
上的最小值和最大值；
上是增函数，求实数
的取值范围．
的准线的方程为
，过点
作倾斜角为
的直线
交该抛物线于两点
，
．求：（1）
的值；（2）弦长
不等式
的解集为Ｒ；命题
：
在区间
上是增函数．若命题“
”为假命题，求实数
的取值范围．
中，已知
，求：
项和
．
作圆C：x2＋y2＝r2(
)的切线，切点为D，且QD＝4．
，求
的最小值(O为坐标原点).推荐套卷
已知二次函数f(x)=x2+ax（）．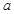
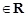（1）若函数y=f(sinx+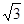cosx)(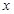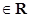)的最大值为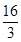，求f(x)的最小值；
（2）当a>2时,求证：f(sin2xlog2sin2x+cos2xlog2cos2x)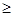1–a.其中x∈R,x¹kp且x¹kp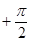(k∈Z).
粤公网安备 44130202000953号