岛A观察站发现在其东南方向有一艘可疑船只，正以每小时10海里的速度向东南方向航行，观察站即刻通知在岛A正南方向B处巡航的海监船前往检查．接到通知后，海监船测得可疑船只在其北偏东75°方向且相距10海里的C处，随即以每小时10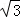
海里的速度前往拦截．
（I）问：海监船接到通知时，距离岛A多少海里？
（II）假设海监船在D处恰好追上可疑船只，求它的航行方向及其航行的时间．
相关试题
，实数
取什么值时，
是纯虚数？
，
在区间（0,+
上恒成立，求
的取值范围；
，其中
．
有极值，求
的取值范围；
，
恒成立，求
的通项公式为
的值；
的值，并用数学归纳法证明你的猜想.推荐套卷
岛A观察站发现在其东南方向有一艘可疑船只，正以每小时10海里的速度向东南方向航行，观察站即刻通知在岛A正南方向B处巡航的海监船前往检查．接到通知后，海监船测得可疑船只在其北偏东75°方向且相距10海里的C处，随即以每小时10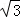 海里的速度前往拦截．
（I）问：海监船接到通知时，距离岛A多少海里？
（II）假设海监船在D处恰好追上可疑船只，求它的航行方向及其航行的时间．
粤公网安备 44130202000953号