当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1①有y=(x-m)2+2m-1②,
所以抛物线顶点坐标为(m,2m-1),即x=m③,y=2m-1④.
当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.
将③代入④,得y=2x-1⑤.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;
根据上述阅读材料提供的方法,确定点(-2m, m-1)满足的函数关系式为_______.
(2)根据阅读材料提供的方法,确定抛物线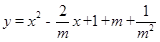 顶点的纵坐标y与横坐标x之间的关系式.
顶点的纵坐标y与横坐标x之间的关系式.