我市某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图（不完整）．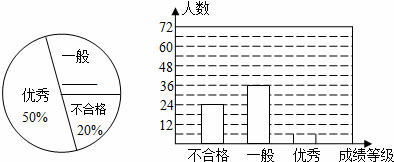
请你根据图中所给的信息解答下列问题：
（1）请将以上两幅统计图补充完整；
（2）若“一般”和“优秀”均被视为达标成绩，则该校被抽取的学生中有 人达标；
（3）若该校学生有1200人，请你估计此次测试中，全校达标的学生有多少人？
相关试题
(本题满分10分)某电视台为了解观众对“谍战”题材电视剧的喜爱情况，随机抽取某社区部分电视观众，进行问卷调查，整理绘制了如下不完整的条形统计图和扇形统计图：
男、女观众对“谍战”题材电视剧的喜爱情况统计图 男观众对“谍战”题材电视剧的喜爱情况统计图
请根据以上信息，解答下列问题：
(1)在这次接受调查的女观众中，表示“不喜欢”的女观众所占的百分比是多少？
(2)求这次调查的男观众人数，并补全条形统计图．
(3)若该社区有男观众约1000人，估计该社区男观众喜欢看“谍战”题材电视剧的约有多少人？
(本题满分8分)甲口袋中装有两个相同的小球，它们分别写有数字4和7；乙口袋装有三个相同的小球，它们分别写有数字5、6、9，小明和小丽玩游戏：从两个口袋中随机地各取出一个小球，如果两个小球上的数字之和是偶数小丽胜；否则小明胜．但小丽认为，这个游戏不公平，你同意小丽的看法吗？用画树形图法或列表法说明现由．
的一元二次方程
（
为常数）
，
为方程的两个实数根，且
，试求出方程的两个实数根和
相关知识点
推荐套卷
粤公网安备 44130202000953号