如图,直线AB过点A(m,0),B(0,n)(其中m>0,n>0).反比例函数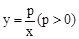 的图象与直线AB交于C,D两点,连接OC,OD.
的图象与直线AB交于C,D两点,连接OC,OD.
(1)已知m+n=10,△AOB的面积为S,问:当n为何值时,S取最大值?并求这个最大值;
(2)若m=8,n=6,当△AOC,△COD,△DOB的面积都相等时,求p的值.
相关知识点
推荐套卷
如图,直线AB过点A(m,0),B(0,n)(其中m>0,n>0).反比例函数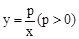 的图象与直线AB交于C,D两点,连接OC,OD.
的图象与直线AB交于C,D两点,连接OC,OD.
(1)已知m+n=10,△AOB的面积为S,问:当n为何值时,S取最大值?并求这个最大值;
(2)若m=8,n=6,当△AOC,△COD,△DOB的面积都相等时,求p的值.