如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．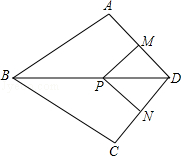
（1）求证：∠ADB=∠CDB；
（2）若∠ADC=90°，求证：四边形MPND是正方形．
．
．
．相关知识点
推荐套卷
如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．
（1）求证：∠ADB=∠CDB；
（2）若∠ADC=90°，求证：四边形MPND是正方形．
粤公网安备 44130202000953号