(1)阅读理解
先观察和计算,并用“>”、“<”、“≥”、“≤”、“=”填空:4+9 2 ,
,
4+4 2 ,2+3 2
,2+3 2 。请猜想:当
。请猜想:当 则
则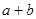
 。
。
如∵ 展开
展开 ∴6+5
∴6+5 。
。
请你给出猜想的一个相仿的说明过程。
(2)知识应用
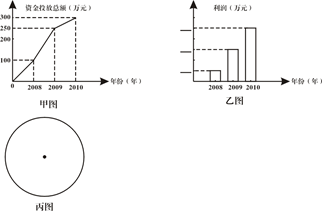
①如图⊙O中,⊙O的半径为5,点P为⊙O内一个定点,OP=2,过点P作两条互相垂直的弦,即AC⊥BD, 作ON⊥BD,OM⊥AC,垂足为M、N,求 的值。
的值。
②在上述基础上,连接AB、BC、CD、DA,利用①中的结论,探求四边形ABCD面积的最大值。
相关知识点
推荐套卷
 +
+ +
+ 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号