某班同学分三组进行数学活动.对七年级400名同学最喜欢的课余生活情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得的:
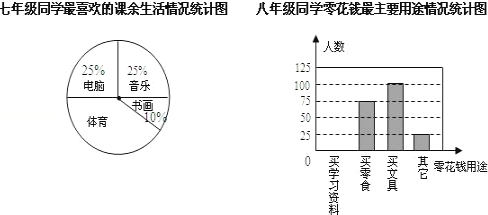
九年级同学完成家庭作业情况统计表
时间
|
1小时左右
|
1.5小时左右
|
2小时左右
|
2.5小时左右
|
人数
|
50
|
80
|
120
|
50
|
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢“体育”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时?(结果保留一位小数)