某校为了解决学生停车难的问题，打算新建一个自行车车棚，图1是车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形．图2是车棚顶部的截面示意图，弧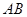
所在圆的圆心为
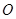，半径
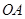为3米.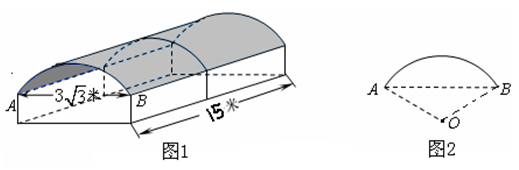
（1）求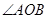
的度数；
（2）学校准备用某种材料制作车棚顶部，请你算一算，需该种材料多少平方米？（不考虑接缝等因素，结果精确到1平方米）.
（第2小题的参考数据：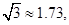
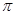取3.14）
，求a、b的值．
ABC中，AD平分
BAC，AB+BD=AC，求
的值．
ABC中，AB=AC，D是BC的中点，
，
，E，F分别是垂足，求证：DE=DF，
，求
的值．
相关知识点
推荐套卷
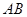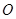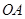某校为了解决学生停车难的问题，打算新建一个自行车车棚，图1是车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形．图2是车棚顶部的截面示意图，弧所在圆的圆心为，半径为3米.
（1）求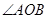的度数；
（2）学校准备用某种材料制作车棚顶部，请你算一算，需该种材料多少平方米？（不考虑接缝等因素，结果精确到1平方米）.
（第2小题的参考数据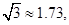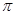：取3.14）
粤公网安备 44130202000953号