如图(1)，∆ABC为等边三角形，AB=6，在直角三角板DEF中∠F=90°，∠FDE=60°，点D在边BC上运动，边DF始终经过点A，DE交AC于点G.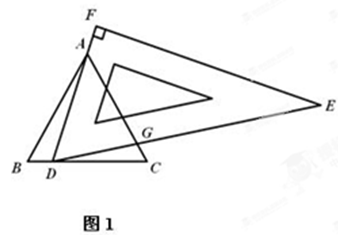
(1)求证:①∠BAD=∠CDG
②∆ABD∽∆DCG
(2)设BD=x,若CG=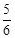
，求x的值；
(3)如图2，当D运动到BC中点时，点P为线段AD上一动点，连接CP，将线段CP绕着点C逆时针旋转60°得到CP' ，连接BP'，DP'，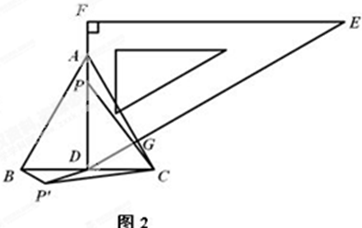
①求∠CBP'的度数；②求DP'的最小值.
相关试题
如图，已知
的顶点
，
，
是坐标原点．将绕点按逆时针旋转90°得到
．写出
两点的坐标；求过
三点的抛物线的解析式，并求此抛物线的顶点
的坐标；在线段
上是否存在点
使得
？若存在，请求出点的坐标；
若不存在，请说明理由．
如图，D,E分别是△ABC的AB,AC边上的点，且DE∥BC,已知AD︰DB=1︰3, DE=2cm,求BC的长.
若△ADE的面积为1.5cm2，求梯形DBCE的面积.
cm, 弓形的高为6cm.
求截面⊙O的半径.
”的方法来确定．已知A站至H站总里程数为1 500千米，全程参考价为180元．下表是沿途各站至H站的里程数：
(元)．
站下车的？（要求写出解答过程）．相关知识点
推荐套卷
粤公网安备 44130202000953号