如图,四边形ABCD、BEFG均为正方形.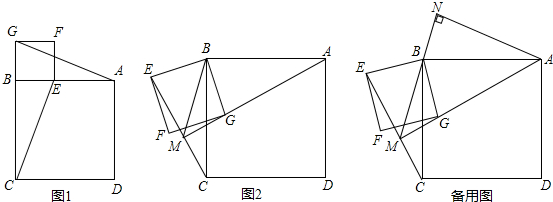
(1)如图1,连接AG、CE,试判断AG和CE的数量关系和位置关系并证明.
(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB的度数;若发生变化,请说明理由.
(3)在(2)的条件下,过点A作AN⊥MB交MB的延长线于点N,请直接写出线段CM与BN的数量关系 .
相关知识点
推荐套卷
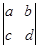 ”称为二阶行列式,规定它的运算法则为:
”称为二阶行列式,规定它的运算法则为: ,请你根据上述规定求出下列等式中
,请你根据上述规定求出下列等式中 的值:
的值: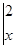
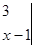 =1.
=1. -
-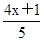 =1
=1 粤公网安备 44130202000953号
粤公网安备 44130202000953号