如图，矩形OABC在平面直角坐标系中，O为坐标原点，点A（0，4），C（2，0），将矩形OABC绕点O按顺时针方向旋转1350，得到矩形EFGH（点E与O重合）.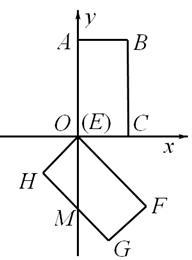
（1）若GH交y轴于点M，则∠FOM＝ ，OM= ；
（2）矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D，若AD∥BO，求t的值；
②若矩形EFHG与矩形OABC重叠部分的面积为S个平方单位，试求当0<t≤
时，S与t之间的函数关系式.
中，∠C=90°.
如图，在平面直角坐标系xOy中，直线AB与x轴交于点A，与y轴交于点B，且OA=3，AB=6．点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AO返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BO-OP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．
（1）求直线AB的解析式；
（2）在点P从O向A运动的过程中（不包括A、O），求△APQ的面积S与t之间的函数关系式，并直接写出t的取值范围；
（3）在点E从B向O运动的过程中，完成下面问题：
四边形QBED能否成为直角梯形？若能，请求出t的值；若不能，请说明理由；
某冰箱厂为响应国家“家电下乡”号召，计划生产
、
两种型号的冰箱100台．经预算，两种冰箱全部售出后，可获得利润不低于 4.75万元，不高于4.8万元，两种型号的冰箱生产成本和售价如下表：
| 型号 |
A型 |
B型 |
| 成本（元/台） |
2200 |
2600 |
| 售价（元/台） |
2800 |
3000 |
（1）冰箱厂有哪几种生产方案？
（2）该冰箱厂按哪种方案生产，才能使投入成本最少？“家电下乡”后农民买家电（冰箱、彩电、洗衣机）可享受13%的政府补贴，那么在这种方案下政府需补贴给农民多少元？
（3）若按（2）中的方案生产，冰箱厂计划将获得的全部利润购买三种物品：体育器材、实验设备、办公用品支援某希望小学．其中体育器材至多买4套，体育器材每套6000元，实验设备每套3000元，办公用品每套1800元，把钱全部用尽且三种物品都购买的情况下，请你直接写出实验设备的买法共有多少种．
如图，直线AB与y轴交于点A,与x轴交于点B，点A的纵坐标、点B的横坐标如图所示．
（1）求直线AB的解析式；
（2）过原点O的直线把△ABO分成面积之比为2:1的两部分，请求出这条直线的解
析式．
粤公网安备 44130202000953号