已知,如图,△AOB的OA、OB两边上的两点M、N.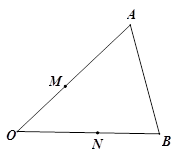
①.求作:点P,使点P到OA、OB的距离相等,且PM=PN.(尺规作图,不写作法,保留作图痕迹)
②.在AB上找一点Q使四边形ONQM周长最小。(不一定尺规作图, 可以用三角尺,不写作法).
相关知识点
推荐套卷
已知,如图,△AOB的OA、OB两边上的两点M、N.
①.求作:点P,使点P到OA、OB的距离相等,且PM=PN.(尺规作图,不写作法,保留作图痕迹)
②.在AB上找一点Q使四边形ONQM周长最小。(不一定尺规作图, 可以用三角尺,不写作法).