用一块钢锭烧铸一个厚度均匀,且表面积为2m2的正四棱锥形有盖容器(如下图)。设容器高为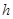 m,盖子边长为
m,盖子边长为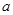 m,
m,
(1)求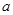 关于
关于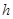 的解析式;
的解析式;
(2)设容器的容积为V m3,则当h为何值时,V最大? 并求出V的最大值(求解本题时,不计容器厚度).
推荐套卷
用一块钢锭烧铸一个厚度均匀,且表面积为2m2的正四棱锥形有盖容器(如下图)。设容器高为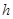 m,盖子边长为
m,盖子边长为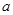 m,
m,
(1)求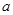 关于
关于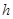 的解析式;
的解析式;
(2)设容器的容积为V m3,则当h为何值时,V最大? 并求出V的最大值(求解本题时,不计容器厚度).