如图，某自来水公司要在公路两侧铺设水管，公路为东西方向，在路北侧沿直线铺设线路l1，在路南侧沿直线铺设线路l2，现要在矩形区域ABCD内沿直线将l1与l2接通．已知AB = 60m，BC = 80m，公路两侧铺设水管的费用为每米1万元，穿过公路的EF部分铺设水管的费用为每米2万元，设∠EFB= α,矩形区域内的铺设水管的总费用为W．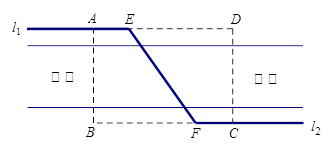
（1）求W关于α的函数关系式；
（2）求W的最小值及相应的角α．
.
在定义域R上的奇偶性与单调性（只须写出结论，无须证明）；
，试证明：
.
的图象在y轴上的截距为1，它在y轴右侧的第一个最大值点和最小值点分别为（
）和（
）.
的解析式；
，求
及
．
求
的关系式及通项公式
推荐套卷
如图，某自来水公司要在公路两侧铺设水管，公路为东西方向，在路北侧沿直线铺设线路l1，在路南侧沿直线铺设线路l2，现要在矩形区域ABCD内沿直线将l1与l2接通．已知AB = 60m，BC = 80m，公路两侧铺设水管的费用为每米1万元，穿过公路的EF部分铺设水管的费用为每米2万元，设∠EFB= α,矩形区域内的铺设水管的总费用为W．
（1）求W关于α的函数关系式；
（2）求W的最小值及相应的角α．
粤公网安备 44130202000953号