（本小题满分13分）
已知菱形ABCD中，AB=4，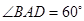 
（如图1所示），将菱形ABCD沿对角线
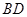翻折，使点
翻折到点
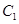的位置（如图2所示），点E，F，M分别是AB，DC1，BC1的中点．
（1）证明：BD //平面
；
（2）证明：
（3）当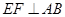
时，求线段AC1的长．
相关试题
的前n项和为
，点
均在函数y＝－x+12的图像上.
的前n项的和.
的两个根，且
。求：(1)角C的度数； (2)AB的长度。
中，侧面
底面
，
,且
,O为
中点.
平面
与平面
所成角的正弦值
推荐套卷
（本小题满分13分）
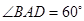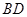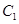已知菱形ABCD中，AB=4， （如图1所示），将菱形ABCD沿对角线翻折，使点翻折到点的位置（如图2所示），点E，F，M分别是AB，DC1，BC1的中点．
（1）证明：BD //平面；
（2）证明：
（3）当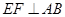时，求线段AC1的长．
粤公网安备 44130202000953号