如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.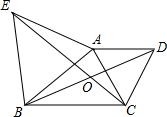
(1)求证:CE=BD;
(2)如果当点A在直线BC的上方变化位置,且保持∠ABC和∠ACB都是锐角,那么∠BOC的度数是否会发生变化?若变化,请说明理由;若不变化,请求出∠BOC的度数:
(3)如果当点A在直线BC的上方变化位置,且保持∠ACB是锐角,那么∠BOC的度数是否会发生变化?若变化,请直接写出变化的结论,不需说明理由;若不变化,请直接写明结论.
相关知识点
推荐套卷
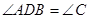 ,
,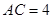 ,
,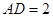 ,
,
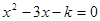 有两个不相等的实数根.
有两个不相等的实数根.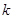 的取值范围;
的取值范围;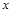 =-2,最高点的纵坐标为4,求:该二次函数解析式。
=-2,最高点的纵坐标为4,求:该二次函数解析式。 时,判断点P是否在直线ME上,说明理由;
时,判断点P是否在直线ME上,说明理由;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号