袋中有8个大小相同的小球，其中1个黑球，3个白球，4个红球.
（I）若从袋中一次摸出2个小球，求恰为异色球的概率；
（II）若从袋中一次摸出3个小球，且3个球中，黑球与白球的个数都没有超过红球的个数，记此时红球的个数为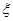
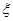，求的分布列及数学期望E.
相关试题
，
，
，且
．
；
与
的夹角为
，求
的值．
中，
，且
，
，
成等差数列．
满足
，求数列
的前n项和
的最大值.已知函数f（x）＝
＋lnx（a＞0）
（1）若函数f（x）在[1，＋∞）上为增函数，求实数a的取值范围；
（2）当a＝1时，求f（x）在[
，2]上的最大值和最小值.
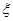（n∈N*），数列{bn}满足2bn＋1＝bn＋bn＋2（n∈N*），且b3＝7，b8＝22.推荐套卷
袋中有8个大小相同的小球，其中1个黑球，3个白球，4个红球.
（I）若从袋中一次摸出2个小球，求恰为异色球的概率；
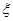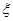（II）若从袋中一次摸出3个小球，且3个球中，黑球与白球的个数都没有超过红球的个数，记此时红球的个数为，求的分布列及数学期望E.
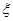已知函数f（x）＝＋lnx（a＞0）
（1）若函数f（x）在[1，＋∞）上为增函数，求实数a的取值范围；
（2）当a＝1时，求f（x）在[，2]上的最大值和最小值.
粤公网安备 44130202000953号