如图，在矩形ABCD中，点E，F分别在线段AB，AD上，AE=EB=AF=
沿直线EF将
翻折成
使平面
平面BEF.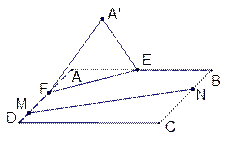
（I）求二面角
的余弦值；
（II）点M，N分别在线段FD，BC上，若沿直线MN将四边形MNCD向上翻折，使C
与
重合，求线段FM的长.
相关试题
以
为圆心且经过原点O,与
轴交于另一点A,与
轴交于另一点B.
为定值
与圆
，若
，求圆
的方程.
-
中，
分别是
,
的中点，
分别是
,
中点，
的体积；
经过直线
与直线
的交点
，且垂直于直线
.
.
.
时，求函数的最大值和最小值；
的取值范围，使
在区间
上是单调函数，并指出相应的单调性．
，
，
，求a的取值范围。推荐套卷
如图，在矩形ABCD中，点E，F分别在线段AB，AD上，AE=EB=AF=沿直线EF将翻折成使平面平面BEF.
（I）求二面角的余弦值；
（II）点M，N分别在线段FD，BC上，若沿直线MN将四边形MNCD向上翻折，使C
与重合，求线段FM的长.
粤公网安备 44130202000953号