已知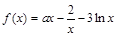
，其中
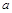为常数.
（Ⅰ）当函数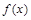
的图象在点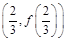
处的切线的斜率为1时，求函数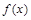在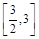
上的最小值；
（Ⅱ）若函数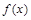在
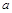上既有极大值又有极小值，求实数的取值范围；
（Ⅲ）在（Ⅰ）的条件下，过点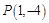
作函数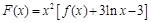
图象的切线，试问这样的切线有几条？并求这些切线的方程.
相关试题
的图像在点
处的切线与直线
平行.
上恒成立，求a的取值范围；
（
）
满足：
的值；
是等比数列； 
（
），如果对任意
，都有
，求实数
的取值范围.推荐套卷
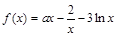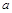已知，其中为常数.
（Ⅰ）当函数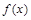的图象在点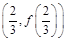处的切线的斜率为1时，求函数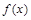在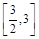上的最小值；
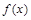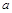（Ⅱ）若函数在上既有极大值又有极小值，求实数的取值范围；
（Ⅲ）在（Ⅰ）的条件下，过点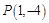作函数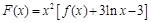图象的切线，试问这样的切线有几条？并求这些切线的方程.
粤公网安备 44130202000953号