已知函数
(a，b均为正常数).
（1）求证：函数
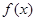在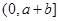
内至少有一个零点；
（2）设函数在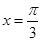
处有极值，
①对于一切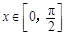
，不等式
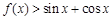恒成立，求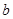
的取值范围；
②若函数f(x)在区间
上是单调增函数，求实数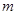
的取值范围.
是奇函数，且
.
的解析式；
上的最小值
，
（
，且
）．
的定义域；
的取值范围
，
，求
，
，
相关知识点
推荐套卷
已知函数(a，b均为正常数).
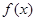（1）求证：函数在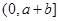内至少有一个零点；
（2）设函数在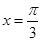处有极值，
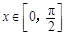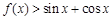①对于一切，不等式恒成立，求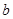的取值范围；
②若函数f(x)在区间上是单调增函数，求实数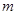的取值范围.
粤公网安备 44130202000953号