如图，在四棱锥P－ABCD中，底面ABCD为直角梯形，且AD∥BC，∠ABC＝∠PAD＝90°，侧面PAD⊥底面ABCD，若PA＝AB＝BC＝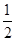
，AD＝1.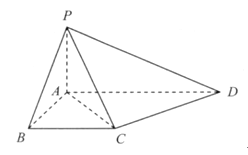
（I）求证：CD⊥平面PAC；
（II）侧棱PA上是否存在点E，使得BE∥平面PCD？若存在，指出点E的位置，并证明，若不存在，请说明理由.
相关试题
，
，
分别是△
和△
的重心．
平面
．
不在同一平面内，求证：
既不平行也不相交．
的上、下两底边长之比为
，连接
，把正三棱台分成三个三棱锥，求这三个三棱锥的体积之比．
的棱长为
，它的四个互不相邻的顶点
，
，
，
构成一个正四面体的顶点，求这个正四面体的体积．
，
，
为三个平面，
，
．求证：
．
推荐套卷
如图，在四棱锥P－ABCD中，底面ABCD为直角梯形，且AD∥BC，∠ABC＝∠PAD＝90°，侧面PAD⊥底面ABCD，若PA＝AB＝BC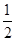＝，AD＝1.
（I）求证：CD⊥平面PAC；
（II）侧棱PA上是否存在点E，使得BE∥平面PCD？若存在，指出点E的位置，并证明，若不存在，请说明理由.
粤公网安备 44130202000953号