为了估计某校的某次数学考试情况，现从该校参加考试的600名学生中随机抽出60名学生，其成绩（百分制）均在
上，将这些成绩分成六段
，
，…
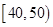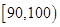，后得到如图所示部分频率分布直方图．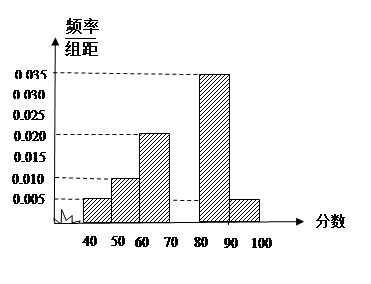
（1）求抽出的60名学生中分数在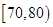
内的人数；
（2）若规定成绩不小于85分为优秀，则根据频率分布直方图，估计该校优秀人数．
相关试题
在
与
处都取得极值。
的解析式；
，且AC=BC.
平面EBC；
的大小.
的面积。
满足：对定义域内任意两个不相等的实数
,都有，则称函数
,且
的值；
,并说明理由.推荐套卷
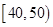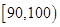为了估计某校的某次数学考试情况，现从该校参加考试的600名学生中随机抽出60名学生，其成绩（百分制）均在上，将这些成绩分成六段，，…，后得到如图所示部分频率分布直方图．
（1）求抽出的60名学生中分数在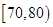内的人数；
（2）若规定成绩不小于85分为优秀，则根据频率分布直方图，估计该校优秀人数．
粤公网安备 44130202000953号