某企业为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的设备维修、燃料和动力等消耗的费用(称为设备的低劣化值)会逐年增加,第一年设备低劣化值是4万元,从第二年到第七年,每年设备低劣化值均比上年增加2万元,从第八年开始,每年设备低劣化值比上年增加25%.
(1)设第 年该生产线设备低劣化值为
年该生产线设备低劣化值为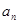 ,求
,求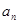 的表达式;
的表达式;
(2)若该生产线前 年设备低劣化平均值为
年设备低劣化平均值为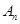 ,当
,当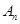 达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
推荐套卷
某企业为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的设备维修、燃料和动力等消耗的费用(称为设备的低劣化值)会逐年增加,第一年设备低劣化值是4万元,从第二年到第七年,每年设备低劣化值均比上年增加2万元,从第八年开始,每年设备低劣化值比上年增加25%.
(1)设第 年该生产线设备低劣化值为
年该生产线设备低劣化值为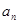 ,求
,求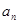 的表达式;
的表达式;
(2)若该生产线前 年设备低劣化平均值为
年设备低劣化平均值为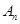 ,当
,当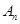 达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.