对于任意的 (
(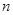 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前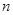 项和等于该数列的前
项和等于该数列的前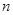 项之积,则称该数列为
项之积,则称该数列为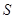 型数列。
型数列。
(1)若数列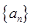 是首项
是首项 的
的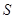 型数列,求
型数列,求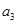 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是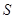 型数列;
型数列;
(3)若数列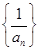 是
是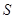 型数列,且
型数列,且 试求
试求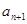 与
与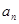 的递推关系,并证明
的递推关系,并证明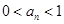 对
对 恒成立。
恒成立。
推荐套卷
对于任意的 (
(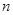 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前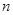 项和等于该数列的前
项和等于该数列的前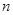 项之积,则称该数列为
项之积,则称该数列为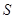 型数列。
型数列。
(1)若数列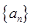 是首项
是首项 的
的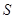 型数列,求
型数列,求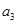 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是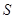 型数列;
型数列;
(3)若数列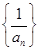 是
是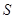 型数列,且
型数列,且 试求
试求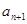 与
与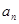 的递推关系,并证明
的递推关系,并证明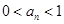 对
对 恒成立。
恒成立。