某饮料公司对一名员工进行测试以便确定其考评级别．公司准备了两种不同的饮料共5 杯，其颜色完全相同，并且其中3杯为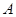
饮料，另外2杯为
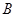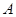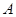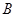饮料，公司要求此员工一一品尝后，从5杯饮料中选出3杯饮料．若该员工3杯都选对，则评为优秀；若3杯选对2杯，则评为良好；否则评为及格．假设此人对和两种饮料没有鉴别能力．
（Ⅰ）求此人被评为优秀的概率；
（Ⅱ）求此人被评为良好及以上的概率．
相关试题
，且
共线，其中
.
的值；
，求
的值.
为从
个不同的元素中取出
个元素的所有组合的个数．随机变量
表示满足
的二元数组
中的
，每一个
（
0，1，2， ，
．
中，
，
，
，动点
满足
，当
时，
．
的长；
的大小为
，求
的值．．
均为正数，证明：
中，圆
的参数方程为
（
为参数）．以原点
轴的非负半轴为极轴的极坐标系中，直线
的极坐标方程为
，直线
相交于
两点，求弦
的长．推荐套卷
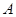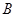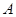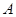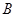某饮料公司对一名员工进行测试以便确定其考评级别．公司准备了两种不同的饮料共5 杯，其颜色完全相同，并且其中3杯为饮料，另外2杯为饮料，公司要求此员工一一品尝后，从5杯饮料中选出3杯饮料．若该员工3杯都选对，则评为优秀；若3杯选对2杯，则评为良好；否则评为及格．假设此人对和两种饮料没有鉴别能力．
（Ⅰ）求此人被评为优秀的概率；
（Ⅱ）求此人被评为良好及以上的概率．
粤公网安备 44130202000953号