已知二次函数h(x)=ax2+bx+c(其中c<3)，其导函数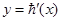
的图象如图，f(x)=6lnx+h(x).
①求f(x)在x=3处的切线斜率；
②若f(x)在区间(m,m+
)上是单调函数，求实数m的取值范围；
③若对任意k∈[-1,1]，函数y=kx(x∈(0,6])的图象总在函数y＝f(x)图象的上方，求c的取值范围.
相关试题
．
的最大值，并求取得最大值时角A、B的大小．
，且
为锐角，求：
的值；
的值．
．
中，
，求其第4项及前5项和.
（
）
的定义域；（2）讨论函数推荐套卷
已知二次函数h(x)=ax2+bx+c(其中c<3)，其导函数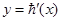的图象如图，f(x)=6lnx+h(x).
①求f(x)在x=3处的切线斜率；
②若f(x)在区间(m,m+)上是单调函数，求实数m的取值范围；
③若对任意k∈[-1,1]，函数y=kx(x∈(0,6])的图象总在函数y＝f(x)图象的上方，求c的取值范围.
粤公网安备 44130202000953号