某学校的校门是伸缩门（如图1），伸缩门中的每一行菱形有20个，每个菱形边长为30厘米．校门关闭时，每个菱形的锐角度数为60°（如图2）；校门打开时，每个菱形的锐角度数从60°缩小为10°（如图3）．问：校门打开了多少米？（结果精确到1米，参考数据：sin5°≈0.0872，cos5°≈0.9962，sin10°≈0.1736，cos10°≈0.9848）．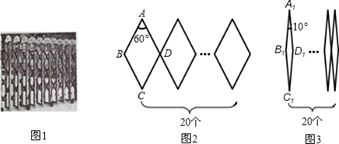
相关试题
(1)求证：△ABC≌△CDE；
的解适
合x＋y＝2，求m的值．
符合条件的点D的坐标；若不存在，请说明理由．
相关知识点
推荐套卷
某学校的校门是伸缩门（如图1），伸缩门中的每一行菱形有20个，每个菱形边长为30厘米．校门关闭时，每个菱形的锐角度数为60°（如图2）；校门打开时，每个菱形的锐角度数从60°缩小为10°（如图3）．问：校门打开了多少米？（结果精确到1米，参考数据：sin5°≈0.0872，cos5°≈0.9962，sin10°≈0.1736，cos10°≈0.9848）．
粤公网安备 44130202000953号