甲，乙，丙三位学生独立地解同一道题，甲做对的概率为
，乙，丙做对的概率分别为
，
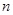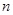(＞)，且三位学生是否做对相互独立.记
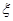为这三位学生中做对该题的人数，其分布列为：
|
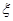0 |
1 |
2 |
3 |
 |
 |
 |
 |
 |
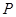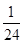(Ⅰ)求至少有一位学生做对该题的概率；
(Ⅱ)求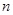，的值；
(Ⅲ)求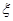的数学期望.
，
，若
且
，求
的值
.
＋f(x)＝0.
, x∈[3, 5]
｝，B={x|
}，求
，
。
，求a；相关知识点
推荐套卷
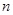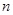甲，乙，丙三位学生独立地解同一道题，甲做对的概率为，乙，丙做对的概率分别为， (＞)，且三位学生是否做对相互独立.记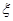为这三位学生中做对该题的人数，其分布列为：
|
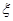0 |
1 |
2 |
3 |
|
|
|
|
|
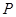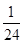(Ⅰ)求至少有一位学生做对该题的概率；
(Ⅱ)求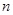，的值；
(Ⅲ)求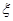的数学期望.
粤公网安备 44130202000953号