某地下车库出口处“两段式栏杆”如图1所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起后的位置如图2所示,其示意图如图3所示,其中AB⊥BC,EF∥BC,∠EAB=1430,AB=AE=1.2米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75.)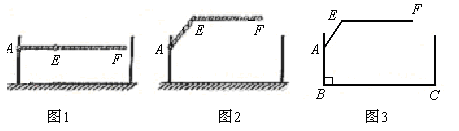
相关知识点
推荐套卷



 粤公网安备 44130202000953号
粤公网安备 44130202000953号