如图,已知直线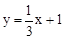 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.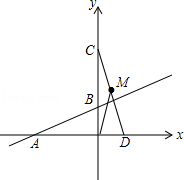
(1)点C的坐标是 ,线段AD的长等于 ;
(2)点M在CD上,且CM=OM,抛物线y=x2+bx+c经过点G,M,求抛物线的解析式;
(3)如果点E在y轴上,且位于点C的下方,点F在直线AC上,那么在(2)中的抛物线上是否存在点P,使得以C,E,F,P为顶点的四边形是菱形?若存在,请求出该菱形的周长l;若不存在,请说明理由.
相关知识点
推荐套卷
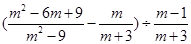
 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点。
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点。
 ,求点F的坐标。
,求点F的坐标。 ,其中
,其中 。
。 ,
, ,其中
,其中 ,若
,若 ,求y与m的函数关系式;
,求y与m的函数关系式; 成立的
成立的 的取值范围.
的取值范围.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号