我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
相关知识点
推荐套卷
 的A1B1C1,并写出点A的对应点A1的坐标;
的A1B1C1,并写出点A的对应点A1的坐标;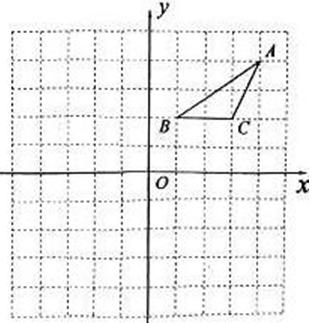
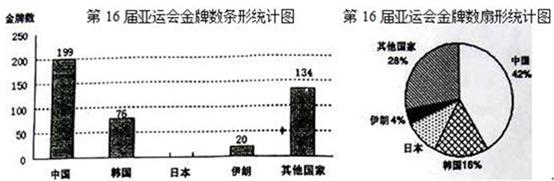
 装床架5个和课桌20套.一辆乙货车可装床架10个和课桌10套.
装床架5个和课桌20套.一辆乙货车可装床架10个和课桌10套. .求
.求
 的度数.(8分)
的度数.(8分)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号