某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率 .设某商品标价为
.设某商品标价为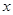 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为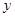 .
.
(Ⅰ)写出当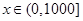 时,
时,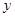 关于
关于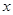 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于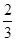 ?
?
推荐套卷
某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率 .设某商品标价为
.设某商品标价为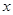 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为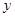 .
.
(Ⅰ)写出当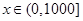 时,
时,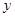 关于
关于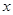 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于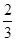 ?
?