若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且|x1|+|x2|=2|k|(k是整数),则称方程x2+bx+c=0为“偶系二次方程”.如方程x2﹣6x﹣27=0,x2﹣2x﹣8=0,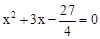 ,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.
,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.
(1)判断方程x2+x﹣12=0是否是“偶系二次方程”,并说明理由;
(2)对于任意一个整数b,是否存在实数c,使得关于x的方程x2+bx+c=0是“偶系二次方程”,并说明理由.
相关知识点
推荐套卷
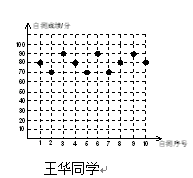
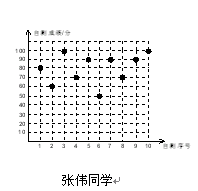

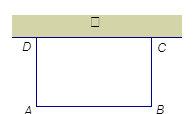
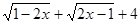
 的值。
的值。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号