如图,已知直线y=x与抛物线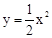 交于A、B两点.
交于A、B两点.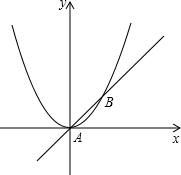
(1)求交点A、B的坐标;
(2)记一次函数y=x的函数值为y1,二次函数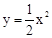 的函数值为y2.若y1>y2,求x的取值范围;
的函数值为y2.若y1>y2,求x的取值范围;
(3)在该抛物线上存在几个点,使得每个点与AB构成的三角形为等腰三角形?并求出不少于3个满足条件的点P的坐标.
相关知识点
推荐套卷
如图,已知直线y=x与抛物线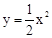 交于A、B两点.
交于A、B两点.
(1)求交点A、B的坐标;
(2)记一次函数y=x的函数值为y1,二次函数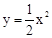 的函数值为y2.若y1>y2,求x的取值范围;
的函数值为y2.若y1>y2,求x的取值范围;
(3)在该抛物线上存在几个点,使得每个点与AB构成的三角形为等腰三角形?并求出不少于3个满足条件的点P的坐标.