如图，在平面直角坐标系xOy中，直线y=x+4与坐标轴分别交于A、B两点，过A、B两点的抛物线为y=﹣x2+bx+c．点D为线段AB上一动点，过点D作CD⊥x轴于点C，交抛物线于点E．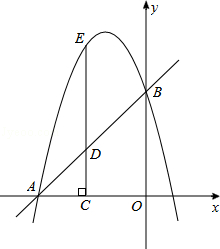
（1）求抛物线的解析式．
（2）当DE=4时，求四边形CAEB的面积．
（3）连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，求此点D坐标；若不存在，说明理由．
相关试题
现在的青少年由于沉迷电视、手机、网络游戏等，视力日渐减退，某市为了解学生的视力变化情况，从全市九年级随机抽取了1500名学生，统计了每个人连续三年视力检查的结果，根据视力在4.9以下的人数变化制成折线统计图，并对视力下降的主要因素进行调查，制成扇形统计图．
解答下列问题：
（1）图中D所在扇形的圆心角度数为；
（2）若2015年全市共有30000名九年级学生，请你估计视力在4.9以下的学生约有多少名？
（3）根据扇形统计图信息，你觉得中学生应该如何保护视力？
有两个相等的实数根．如图，在△ABC中，∠C=60°，∠A=40°．
（1）用尺规作图作AB的垂直平分线，交AC于点D，交AB于点E（保留作图痕迹，不要求写作法和证明）；
（2）求证：BD平分∠CBA．
如图，在平面直角坐标系中，抛物线
，经过A（0，﹣4），B（
，0），C（
，0）三点，且
．
（1）求b，c的值；
（2）在抛物线上求一点D，使得四边形BDCE是以BC为对角线的菱形；
（3）在抛物线上是否存在一点P，使得四边形BPOH是以OB为对角线的菱形？若存在，求出点P的坐标，并判断这个菱形是否为正方形？若不存在，请说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号