一个口袋中装有2个白球和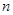 个红球(
个红球(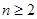 且
且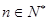 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(Ⅰ) 摸球一次,若中奖概率为 ,求
,求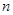 的值;
的值;
(Ⅱ) 若 ,摸球三次,记中奖的次数为
,摸球三次,记中奖的次数为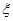 ,试写出
,试写出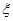 的分布列并求其期望.
的分布列并求其期望.
推荐套卷
一个口袋中装有2个白球和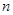 个红球(
个红球(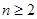 且
且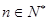 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(Ⅰ) 摸球一次,若中奖概率为 ,求
,求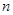 的值;
的值;
(Ⅱ) 若 ,摸球三次,记中奖的次数为
,摸球三次,记中奖的次数为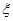 ,试写出
,试写出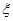 的分布列并求其期望.
的分布列并求其期望.