某校为培育青少年科技创新能力，举办了动漫制作活动，小明设计了点做圆周运动的一个雏形，如图所示，甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动，甲运动的路程l（cm）与时间t（s）满足关系：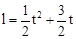
（t≥0），乙以4cm/s的速度匀速运动，半圆的长度为21cm．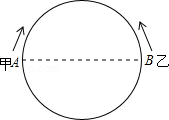
（1）甲运动4s后的路程是多少？
（2）甲、乙从开始运动到第一次相遇时，它们运动了多少时间？
（3）甲、乙从开始运动到第二次相遇时，它们运动了多少时间？
，
的值．（2）
的值．
（2）
，其中
（2）
（x>0）图象于点A、B，交x轴于点C．（1）求m的取值范围；（2）若点A的坐标是（2，－4），且
，求m的值和C点的坐标；
相关知识点
推荐套卷
某校为培育青少年科技创新能力，举办了动漫制作活动，小明设计了点做圆周运动的一个雏形，如图所示，甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动，甲运动的路程l（cm）与时间t（s）满足关系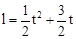：（t≥0），乙以4cm/s的速度匀速运动，半圆的长度为21cm．
（1）甲运动4s后的路程是多少？
（2）甲、乙从开始运动到第一次相遇时，它们运动了多少时间？
（3）甲、乙从开始运动到第二次相遇时，它们运动了多少时间？
粤公网安备 44130202000953号